해당 논문은 2016년 CVPR에 Microsoft Research에서 발표한 논문입니다.
논문에 대한 전문을 보시려면 여기를 클릭하세요.
혹시 잘못된 내용이 있으면 언제든지 댓글 부탁드립니다!
최근 프로젝트 내용들을 정리하다가 residual connections이 어떻게 degradation 문제를 해결할 수 있었는지에 대해 알기 위해 작성했습니다.

글을 작성하는 시점인 8월 12일 기준으로 약 85000회 인용이 된 논문입니다. 그만큼 중요한 논문이라고 할 수 있습니다. 논문 내용은 Abstract부분부터 순차적으로 정리했으나, 일부 겹치는 부분들이 있습니다. 또한 Related Work에 대한 내용들은 다루지 않은 부분도 있으니 참고하시면 좋을 것 같습니다.
1. 논문 정리
Abstract
Neural network가 깊어질수록 학습하기 어렵다고 언급하면서 해당 논문에서는 학습하기 쉽도록 하는 residual learning framework를 제안합니다. 이들이 제안한 residual network는 이전의 네트워크들에 비해 optimize하기 쉬우며, 깊은 layer를 쌓아서 좋은 정확도를 얻어낼 수 있다고 언급합니다. 특히 152 layer로 구성된 resnet은 VGG Net과 비교하며 8배 깊은 네트워크를 가지지만 복잡도는 낮습니다. 또한 이들이 제안한 모델은 다양한 데이터셋에서 활용하여 좋은 성능을 얻을 수 있었습니다. 이미지 분류뿐만 아니라 object detection, segmentation task에서도 좋은 성능을 보였습니다.
(1) 기존 문제
이미지 분류 문제에서 신경망을 깊게 쌓는 것은 feature들의 level을 풍부하게 하는 역할을 합니다. VGG 논문과 GoogleNet 논문에서도 네트워크의 깊이가 중요하다고 언급합니다. 논문에서는 "단순히 깊은 네트워크를 쌓는 것이 더 좋은 네트워크를 학습할 수 있는 것인가?"에 대한 의문을 가지게 되었습니다. 이전의 연구들에서 단순히 깊게 네트워크를 쌓는 것은 다양한 문제를 발생시킬 수 있다고 알려져 왔습니다. 그 대표적인 문제 중 하나가 gradient vanishing/exploding 현상입니다. 이 문제는 네트워크의 가중치 값들을 적절하게 초기화해주는 방법과 layer norm을 통해 어느 정도 해결해왔습니다. 본문의 저자는 네트워크가 깊어짐에 따라 degradation 문제가 발생할 수 있다고 주장하고 있습니다. 여기서 degradation 문제는 layer가 깊어지면서 train과 test가 학습이 되지 않는 현상을 말합니다. 쉽게 말해 적은 layer의 네트워크보다 높은 error를 갖게 되는 것을 말합니다. 이 문제는 overfitting으로 발생하는 문제는 아닙니다. overfitting의 경우 train은 잘되지만 test에서 error가 높아지는 현상인데 여기서 언급하고 있는 degradation 문제와는 다릅니다.

위의 그림처럼 20 layer를 쌓은 네트워크에 비해 train과 테스트 모두 높은 error를 갖는 것이 degradation 문제라고 이야기하고 있습니다.
(2) Residual Connections
논문의 저자는 layer를 깊게 쌓기 위해서 네트워크에 존재하는 다양한 layer가 identity mapping을 가진다면, shallower network에 비해 deeper network가 더 낮은 training error를 가져야 한다고 말합니다. 그래서 해당 논문에서는 $H(x)$를 바로 학습하기보다는 $F(x) := H(x) - x$로 만드는 $F(x)$를 학습하는 방향으로 문제를 풀려고 합니다. 만약, identity mapping이 최적의 mapping이라고 한다면, 해당 $F(x)$를 0으로 fitting 시키는 것으로 문제를 풀 수 있게 됩니다. 이렇게 했을 때, $H(x)$를 $x$로 fitting 하는 것보다 쉽게 학습할 수 있다고 말합니다. 결과적으로 "shortcut connections"은 결과 $F(x)$에다가 $x$를 더하는 것을 말하며, 다른 논문에서는 "skip connections"이라고 하기도 합니다. 위에서 언급한 "shortcut connections"는 단순히 $x$를 더해주는 과정이기 때문에 간단하게 적용할 수 있고, 추가적인 파라미터나 복잡도는 증가하지 않는 장점이 있습니다.

위의 그림처럼 2개의 weight layer들을 $F(x)$로 만들어서 $F(x)$에 대한 정보만 학습할 수 있도록 하고, $x$는 이전의 input을 그대로 넣어주도록 해서 자연스럽게 identity mapping을 수행할 수 있도록 합니다. 또한 $F(x)$와 $x$의 dimension이 일치하지 않을 때에는 linear projection $W_{s}$를 $x$에 곱해서 다음과 같은 식으로 맞춰줄 수 있습니다.
$$ y = F(x, {W_{i}}) + W_{s}x$$
추가적으로, 논문에서는 linear projection을 사용하지 않아도 충분한 성능이 나온다는 것을 언급하고 있습니다. 또한 $F(x)$를 구성할 때, 1개의 layer를 사용하게 되면 $ y = W_{1}x + x = (W_{1}+1)x$가 되어, 앞에서 언급했던 shortcut connections으로 인한 이점을 잃어버리게 됩니다. 그래서 $W$가 여러 개 중첩된 상태에서 사용했을 때, 유의미한 성능이 있었다고 합니다.

위의 그림처럼 VGG-19를 기본 모델로 잡아서 34 layer짜리 plain network와 residual network를 구성했습니다. VGG-19의 FLOPs는 19.6 billion이고, plain과 residual의 경우 3.6 billion으로 확실히 복잡도가 낮은 것을 확인할 수 있습니다. 여기서 FLOPs는 딥러닝 모델의 계산 복잡도를 계산하기 위한 Metric입니다. residual network에서 화살표는 residual connections을 표현한 것이고, 점선으로 된 화살표는 dimension이 달라져서 이를 맞춰주기 위한 linear projection이 포함된 connection입니다.

좌측은 plain network를 사용했을 때, 평가 결과이고 우측은 residual network를 사용했을 때의 결과입니다. 좌측은 residual connections이 적용되지 않아 degradation 현상이 발생하는 모습을 볼 수 있었습니다. 반면, residual network에서는 깊어질수록 더 낮은 error를 보이는 것을 확인할 수 있습니다. 이를 통해, residual connections이 degradation 문제를 해결한 것으로 볼 수 있습니다.
모델이 깊어질수록 학습이 되지 않는 현상은 gradient vanishing 현상 때문에 발생한 것은 아니라고 이야기하고 있습니다. 그 근거로 forward와 backward를 살펴본 결과 vanishing 현상이 일어나지 않았다고 말합니다. 저자들은 이러한 degradation 현상이 발생한 이유를 기하급수적으로 수렴률이 줄어드는 것 때문이라고 이야기하고 있습니다. (수렴률 : 최적화 기법에서 사용되는 개념, 수렴을 위해 필요한 에폭이나 수렴 난이도를 나타내는 지표)
(3) Bottleneck

위의 그림은 파라미터 수를 줄이기 위해 $3 \times 3$ Conv layer 2개를 $1 \times 1$ Conv layer와 $3 \times 3$ Conv layer와 $1 \times 1$ Conv layer로 바꿨습니다. 왼쪽의 input이 64 channel이고 output이 64 channel인 kernel 3짜리 conv layer 2개의 연산량은 $input \, channel \times output \, channel \times (kernel \, size)^{2}$로 73728번이 나오게 됩니다. 반면 우측의 경우, dimension크기가 256으로 커졌음에도 69632번의 연산량을 얻을 수 있습니다.

위의 Table에서 보시는 것처럼 18 layer와 34 layer 부분에서는 $3 \times 3$ Conv layer 2개 사용했고, 50 layer 이상에서는 위에서 언급했던 bottleneck 방법을 활용했습니다. FLOPs를 확인해보시면, 34와 50이 크게 차이가 안나는 것을 봤을 때, bottleneck이 FLOPs 측면에서 좋은 역할을 했다고 볼 수 있습니다.
(개인적인 생각) 다만, 여기서 의문이 드는 부분은 좌측에 비해 확실하게 연산량은 줄어들었으나, conv layer 2개를 연산한 것보다 receptive field 측면에서는 줄어들게 되는데 이 부분에서는 좌측이 좀 더 feature를 잘 뽑아내겠지만 연산량과 성능의 trade off로 볼 수 있을 것 같습니다.
(4) 결과
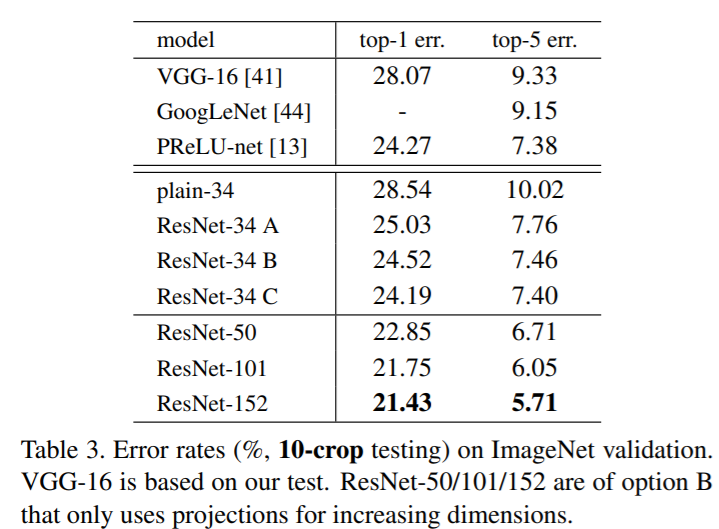
결과적으로 ImageNet Validation을 진행했을 때, Error를 비교해보면 확실하게 plain에 비해 error가 떨어진 것을 확인할 수 있습니다. 중간에 34 layer에 대해 (A), (B), (C)를 다르게 줬는데, (A)는 zero-padding을 통해서 shortcut의 dimension을 맞춰주는 방법이고, (B)는 projection shortcut을 dimension이 바뀔 때만 적용한 방법이며, (C)는 projection shortcut을 모든 residual connection에 적용한 방법입니다. (C)가 (A), (B)에 비해 성능개선이 조금은 있으나, 크게 유의미하다고 판단하지는 않아 50 layer, 101 layer, 152 layer에는 (B) 방법을 적용했습니다.
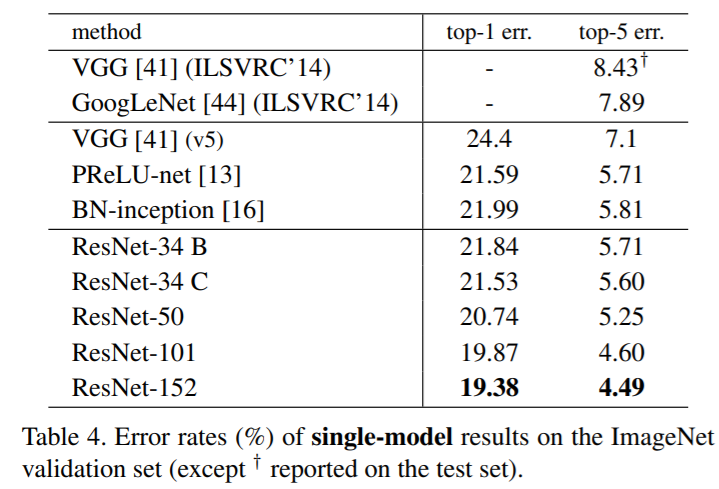
Table 4는 ImageNet 데이터에 대한 단일 모델 성능을 표현한 것으로, 확실히 layer가 깊어질수록 error가 줄어드는 것을 확인할 수 있었습니다.

Table 5는 최종 앙상블한 결과로 최고의 성능을 뽑았다는 것을 보여주고 있습니다. 이 외에도 다양한 데이터셋과 Task에도 적용했을 때, 좋은 성능을 보였습니다.
2. 세줄 요약
- Degradation 문제를 해결하기 위해 residual connection을 적용했다.
- 네트워크가 깊어짐에 따라 증가하는 복잡도를 줄이기 위해 Bottleneck을 적용했다.
- 해당 시기의 Image classification, Object detection, Semantic Segmentation 등의 task에서 좋은 성능을 보여줬다.