아래의 그림은 Mathematics for Machine Learning이라는 책에서 발췌한 그림입니다. 차원 축소를 이해하기 위해 어떠한 개념들이 필요한 지 표현하고 있는 그림입니다.
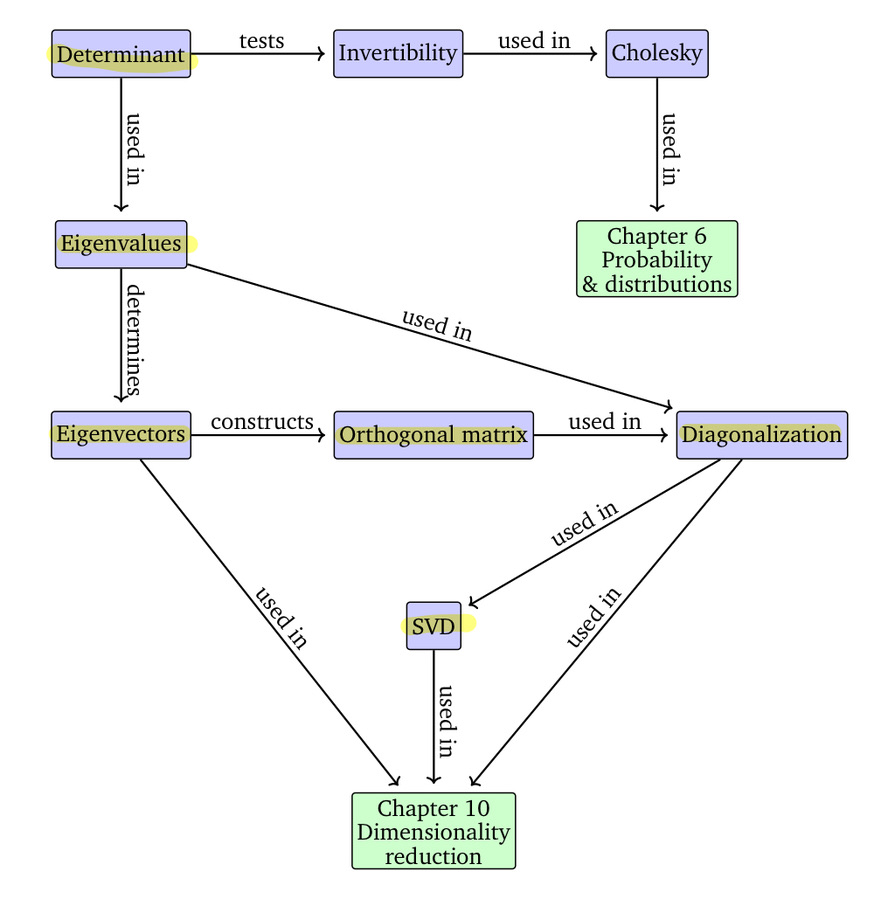
지난 포스팅에서 determinant에 대해 다뤄봤습니다. 오늘은 선형대수학에서 가장 중요한 부분을 담당하는 eigenvalue, eigenvector과 diagonalzation에 대해 소개해보도록 하겠습니다.
1. EigenValue, EigenVector
Eigenvalue(고윳값), Eigenvector(고유 벡터)는 앞에서 이야기했듯이, 선형대수학에서 중요한 개념입니다. Eigenvalue는 인구 성장, 미분방정식, 공학, 과학 등에서 기본이 되는 개념이라 그런지 많이 중요한 것 같습니다. 그러면, 각각에 대한 정의를 아래에서 소개해보겠습니다.
Eigenvalue, Eigenvector 정의
$A$ 를 $n \times n$ 정방행렬이라고 가정해봅시다. $x$를 $n \times 1$ 행렬이라고 했을 때, 아래의 수식이 만족되었을 때, $ \lambda $는 상수로 Eigenvalue, $ x $ 를 Eigenvector라고 합니다. 이때, $x$는 영 벡터가 아니어야 합니다.
$$ Ax = \lambda x $$
위의 수식을 만족하는 Eigenvalue와 Eigenvector가 존재하기 위해서는 $ (\lambda I - A)$가 역행렬이 존재하지 않아야 합니다(singular). 역행렬이 존재하지 않는다면, 이전 포스팅에서 다뤘던 determinant로 표현해보면, $det(\lambda I - A) = 0$을 만족해야 합니다. $det(\lambda I - A) = 0 $의 식은 특성방정식(characteristic equation)이라고 불립니다.
하나의 예시를 통해서 직접 Eigenvalue, Eigenvector를 구해봅시다.
$$ A = \begin{bmatrix} 1 & 4 \\ 2 & 3 \end{bmatrix}$$
위의 행렬의 특정방정식을 구해보면,
$$ | \lambda I - A | = \begin{vmatrix} \lambda - 1 & -4 \\ -2 & \lambda -3 \end{vmatrix} $$
$$ | \lambda I - A | = {\lambda}^2 - 4 \lambda + 3 - 8 = 0 $$
$$ | \lambda I - A | = {\lambda}^2 - 4 \lambda - 5 = (\lambda - 5)(\lambda + 1) = 0 $$
위의 특정방정식을 만족하는 $\lambda$의 해는 5, -1입니다.
그러면, ${\lambda}_{1} = 5$일 때의 eigenvector를 구해봅시다.
$$ \begin{bmatrix} 5 - 1 & 0 - 4 \\ 0 - 2 & 5 - 3 \end{bmatrix} = \begin{bmatrix} 4 & -4 \\ -2 & 2 \end{bmatrix} $$
$$ \begin{bmatrix} 4 & -4 \\ -2 & 2 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} $$
$ 4x - 4y = 0, -2x + 2y = 0$ 이고, eigenvector는 영 벡터가 아니므로, $x = y$ 를 만족해야 합니다. 따라서, ${\lambda}_{1}$의 고유 벡터는 $ {v}_{1} = \begin{bmatrix} 1 \\ 1 \end{bmatrix}$ 로 표현할 수 있습니다.
이번에는 ${\lambda}_{2} = -1$일 때의 eigenvector를 구해봅시다.
$$ \begin{bmatrix} -1 -1 & 0 - 4 \\ 0 - 2 & -1 - 3 \end{bmatrix} = \begin{bmatrix} -2 & -4 \\ -2 & -4 \end{bmatrix} $$
$$ \begin{bmatrix} -2 & -4 \\ -2 & -4 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} $$
$ -2x - 4y = 0$이고, eigenvector는 영벡터가 아니므로, $x=-2y$를 만족해야 합니다. 따라서, ${\lambda}_{2}$의 고유 벡터는 ${v}_{2} = \begin{bmatrix} 2 \\ -1 \end{bmatrix} $로 표현할 수 있습니다.
위의 방법처럼 $A$라는 정방행렬이 주어졌을 때, $\lambda$(고윳값)을 구하기 위해, $det(\lambda I - A) = 0$인 특정 방정식의 해를 구하고, 각 $\lambda$ 값에 맞는 고유 벡터를 구해주면 됩니다.
2. Diagonalization
Diagonalization은 대각화로 정방행렬 $A$가 존재할 때, $A = PD{P}^{-1}$로 표현이 가능할 때, diagonalizable 하다고 합니다. 이때, $A$와 $D$는 유사(similar) 해야 하며, $D$는 대각성분만 존재하는 diagonal matrix여야 합니다.
그러면 여기서 말하는 유사(similar)하다는 것은 무슨 뜻일까요? $A$와 $A'$이 둘다 n차 정방 행렬일 때, similar 하다는 것은 가역 행렬(역행렬이 존재) $P$에 의해 $ A' = {P}^{-1} A P $를 만족할 때를 말합니다. 이때, $A'$은 diagonal matrix입니다. 위의 diagonlization의 수식의 $D$에 해당되는 부분이 $A'$과 같습니다.
여기서 가역행렬을 앞뒤에 곱하는 것이 어떠한 유익을 줄까요? 바로, 계산을 쉽게 할 수 있다는 장점이 있습니다. 예를 들어, $A$ 행렬을 3번 곱한 값이 궁금하다고 했을 때, $A^{3}$ 대신 $(PD{P}^{-1})(PD{P}^{-1})(PD{P}^{-1})$을 계산할 수 있습니다. $P$와 ${P}^{-1}$은 곱하면, 항등 행렬이 되므로 간단하게 표현하면, $P{D}^{3}{P}^{-1}$로 표현할 수 있습니다.
대각행렬의 곱셈은 대각 성분의 3 제곱으로 표현할 수 있습니다.
예를 들어, $A = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 3 \end{bmatrix}$라고 했을 때, 실제 계산해보면, 아래와 같은 결과를 얻을 수 있습니다.
$$ A^{2} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 3 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 3 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 4 & 0 \\ 0 & 0 & 9 \end{bmatrix} $$
이러한 이유로 행렬을 쪼개는 방식을 사용합니다. 나중에 소개할 행렬 분해에서도 동일한 방법을 활용합니다.
그렇다면, $P$ 행렬은 어떻게 구할 수 있을까? 바로 eigenvector들로 만들 수 있습니다.
한 가지 예시로, $A$는 대각화 가능한 행렬이라고 해봅시다. $A$를 대각화하는 행렬 $P$를 구해봅시다.
$$ A = \begin{bmatrix} 1 & -1 & -1 \\ 1 & 3 & 1 \\ -3 & 1 & -1 \end{bmatrix} $$
먼저, 대각화 가능하다고 했으니, 대각성분에 해당하는 eigenvalue를 먼저 구해봅시다.
$$ | \lambda I - A | = \begin{vmatrix} \lambda - 1 & 1 & 1 \\ -1 & \lambda - 3 & -1 \\ 3 & -1 & \lambda + 1 \end{vmatrix} = (\lambda - 2)(\lambda + 2)(\lambda - 3) $$
위의 결과로 eigenvalue 값은 2, -2, 3의 값을 가지게 됩니다. 각각의 eigenvector를 구해보면 아래와 같습니다.
$\lambda = 2$ 일 때
$$ 2 I - A = \begin{bmatrix} 1 & 1 & 1 \\ -1 & -1 & -1 \\ 3 & -1 & 3 \end{bmatrix} $$
위의 수식을 determinant 연산에 의해서 간단하게 표현하면 아래와 같은 수식을 만들 수 있습니다.
$$ 2 I - A = \begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{bmatrix} $$
$ x = -z $, $y = 0$의 수식을 만족해야 하므로, $\lambda = 2$일 때의 eigenvector는 $\begin{bmatrix} -1 \\ 0 \\ 1 \end{bmatrix} $가 됩니다.
동일한 방식으로 3개의 eigenvector를 구해보면,
$$ \lambda_{1} = 2, v_{1} = \begin{bmatrix} -1 \\ 0 \\ 1 \end{bmatrix} $$
$$ \lambda_{2} = -2, v_{2} = \begin{bmatrix} 1 \\ -1 \\ 4 \end{bmatrix} $$
$$ \lambda_{3} = 3, v_{3} = \begin{bmatrix} -1 \\ 1 \\ 1 \end{bmatrix} $$
이렇게 얻어진 벡터들을 합치면 아래와 같이 $P$ 행렬을 구할 수 있습니다.
$$ P = \begin{bmatrix} -1 & 1 & -1 \\ 0 & -1 & 1 \\ 1 & 4 & 1 \end{bmatrix} $$
위의 $P$를 가지고 $P^{-1}$를 구해서 $P^{-1}AP$를 구하면 아래와 같은 값을 얻게 됩니다.
$$D = P^{-1} A P = \begin{bmatrix} 2 & 0 & 0 \\ 0 & -2 & 0 \\ 0 & 0 & 3 \end{bmatrix} $$
결과를 살펴보면, $P$를 구성할 때, eigenvector의 순서에 따라, eigenvalue가 위치하는 것을 볼 수 있습니다.
$$ P = \begin{bmatrix} v_{1} & v_{2} & v_{3} \end{bmatrix}, D = \begin{bmatrix} \lambda_{1} & 0 & 0 \\ 0 & \lambda_{2} & 0 \\ 0 & 0 & \lambda_{3} \end{bmatrix} $$
앞에서 배웠던 eigenvalue 구하는 방법을 통해서 대각화를 진행하는 방법까지 알아봤습니다. 다음 포스팅에서는 SVD와 orthogonal, orthonormal에 대해 소개해보려고 합니다. 조금이나마 도움이 되셨길 바랍니다.
아래의 그림은 Mathematics for Machine Learning이라는 책에서 발췌한 그림입니다. 차원 축소를 이해하기 위해 어떠한 개념들이 필요한 지 표현하고 있는 그림입니다.

지난 포스팅에서 determinant에 대해 다뤄봤습니다. 오늘은 선형대수학에서 가장 중요한 부분을 담당하는 eigenvalue, eigenvector과 diagonalzation에 대해 소개해보도록 하겠습니다.
1. EigenValue, EigenVector
Eigenvalue(고윳값), Eigenvector(고유 벡터)는 앞에서 이야기했듯이, 선형대수학에서 중요한 개념입니다. Eigenvalue는 인구 성장, 미분방정식, 공학, 과학 등에서 기본이 되는 개념이라 그런지 많이 중요한 것 같습니다. 그러면, 각각에 대한 정의를 아래에서 소개해보겠습니다.
Eigenvalue, Eigenvector 정의
$A$ 를 $n \times n$ 정방행렬이라고 가정해봅시다. $x$를 $n \times 1$ 행렬이라고 했을 때, 아래의 수식이 만족되었을 때, $ \lambda $는 상수로 Eigenvalue, $ x $ 를 Eigenvector라고 합니다. 이때, $x$는 영 벡터가 아니어야 합니다.
$$ Ax = \lambda x $$
위의 수식을 만족하는 Eigenvalue와 Eigenvector가 존재하기 위해서는 $ (\lambda I - A)$가 역행렬이 존재하지 않아야 합니다(singular). 역행렬이 존재하지 않는다면, 이전 포스팅에서 다뤘던 determinant로 표현해보면, $det(\lambda I - A) = 0$을 만족해야 합니다. $det(\lambda I - A) = 0 $의 식은 특성방정식(characteristic equation)이라고 불립니다.
하나의 예시를 통해서 직접 Eigenvalue, Eigenvector를 구해봅시다.
$$ A = \begin{bmatrix} 1 & 4 \\ 2 & 3 \end{bmatrix}$$
위의 행렬의 특정방정식을 구해보면,
$$ | \lambda I - A | = \begin{vmatrix} \lambda - 1 & -4 \\ -2 & \lambda -3 \end{vmatrix} $$
$$ | \lambda I - A | = {\lambda}^2 - 4 \lambda + 3 - 8 = 0 $$
$$ | \lambda I - A | = {\lambda}^2 - 4 \lambda - 5 = (\lambda - 5)(\lambda + 1) = 0 $$
위의 특정방정식을 만족하는 $\lambda$의 해는 5, -1입니다.
그러면, ${\lambda}_{1} = 5$일 때의 eigenvector를 구해봅시다.
$$ \begin{bmatrix} 5 - 1 & 0 - 4 \\ 0 - 2 & 5 - 3 \end{bmatrix} = \begin{bmatrix} 4 & -4 \\ -2 & 2 \end{bmatrix} $$
$$ \begin{bmatrix} 4 & -4 \\ -2 & 2 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} $$
$ 4x - 4y = 0, -2x + 2y = 0$ 이고, eigenvector는 영 벡터가 아니므로, $x = y$ 를 만족해야 합니다. 따라서, ${\lambda}_{1}$의 고유 벡터는 $ {v}_{1} = \begin{bmatrix} 1 \\ 1 \end{bmatrix}$ 로 표현할 수 있습니다.
이번에는 ${\lambda}_{2} = -1$일 때의 eigenvector를 구해봅시다.
$$ \begin{bmatrix} -1 -1 & 0 - 4 \\ 0 - 2 & -1 - 3 \end{bmatrix} = \begin{bmatrix} -2 & -4 \\ -2 & -4 \end{bmatrix} $$
$$ \begin{bmatrix} -2 & -4 \\ -2 & -4 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} $$
$ -2x - 4y = 0$이고, eigenvector는 영벡터가 아니므로, $x=-2y$를 만족해야 합니다. 따라서, ${\lambda}_{2}$의 고유 벡터는 ${v}_{2} = \begin{bmatrix} 2 \\ -1 \end{bmatrix} $로 표현할 수 있습니다.
위의 방법처럼 $A$라는 정방행렬이 주어졌을 때, $\lambda$(고윳값)을 구하기 위해, $det(\lambda I - A) = 0$인 특정 방정식의 해를 구하고, 각 $\lambda$ 값에 맞는 고유 벡터를 구해주면 됩니다.
2. Diagonalization
Diagonalization은 대각화로 정방행렬 $A$가 존재할 때, $A = PD{P}^{-1}$로 표현이 가능할 때, diagonalizable 하다고 합니다. 이때, $A$와 $D$는 유사(similar) 해야 하며, $D$는 대각성분만 존재하는 diagonal matrix여야 합니다.
그러면 여기서 말하는 유사(similar)하다는 것은 무슨 뜻일까요? $A$와 $A'$이 둘다 n차 정방 행렬일 때, similar 하다는 것은 가역 행렬(역행렬이 존재) $P$에 의해 $ A' = {P}^{-1} A P $를 만족할 때를 말합니다. 이때, $A'$은 diagonal matrix입니다. 위의 diagonlization의 수식의 $D$에 해당되는 부분이 $A'$과 같습니다.
여기서 가역행렬을 앞뒤에 곱하는 것이 어떠한 유익을 줄까요? 바로, 계산을 쉽게 할 수 있다는 장점이 있습니다. 예를 들어, $A$ 행렬을 3번 곱한 값이 궁금하다고 했을 때, $A^{3}$ 대신 $(PD{P}^{-1})(PD{P}^{-1})(PD{P}^{-1})$을 계산할 수 있습니다. $P$와 ${P}^{-1}$은 곱하면, 항등 행렬이 되므로 간단하게 표현하면, $P{D}^{3}{P}^{-1}$로 표현할 수 있습니다.
대각행렬의 곱셈은 대각 성분의 3 제곱으로 표현할 수 있습니다.
예를 들어, $A = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 3 \end{bmatrix}$라고 했을 때, 실제 계산해보면, 아래와 같은 결과를 얻을 수 있습니다.
$$ A^{2} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 3 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 3 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 4 & 0 \\ 0 & 0 & 9 \end{bmatrix} $$
이러한 이유로 행렬을 쪼개는 방식을 사용합니다. 나중에 소개할 행렬 분해에서도 동일한 방법을 활용합니다.
그렇다면, $P$ 행렬은 어떻게 구할 수 있을까? 바로 eigenvector들로 만들 수 있습니다.
한 가지 예시로, $A$는 대각화 가능한 행렬이라고 해봅시다. $A$를 대각화하는 행렬 $P$를 구해봅시다.
$$ A = \begin{bmatrix} 1 & -1 & -1 \\ 1 & 3 & 1 \\ -3 & 1 & -1 \end{bmatrix} $$
먼저, 대각화 가능하다고 했으니, 대각성분에 해당하는 eigenvalue를 먼저 구해봅시다.
$$ | \lambda I - A | = \begin{vmatrix} \lambda - 1 & 1 & 1 \\ -1 & \lambda - 3 & -1 \\ 3 & -1 & \lambda + 1 \end{vmatrix} = (\lambda - 2)(\lambda + 2)(\lambda - 3) $$
위의 결과로 eigenvalue 값은 2, -2, 3의 값을 가지게 됩니다. 각각의 eigenvector를 구해보면 아래와 같습니다.
$\lambda = 2$ 일 때
$$ 2 I - A = \begin{bmatrix} 1 & 1 & 1 \\ -1 & -1 & -1 \\ 3 & -1 & 3 \end{bmatrix} $$
위의 수식을 determinant 연산에 의해서 간단하게 표현하면 아래와 같은 수식을 만들 수 있습니다.
$$ 2 I - A = \begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{bmatrix} $$
$ x = -z $, $y = 0$의 수식을 만족해야 하므로, $\lambda = 2$일 때의 eigenvector는 $\begin{bmatrix} -1 \\ 0 \\ 1 \end{bmatrix} $가 됩니다.
동일한 방식으로 3개의 eigenvector를 구해보면,
$$ \lambda_{1} = 2, v_{1} = \begin{bmatrix} -1 \\ 0 \\ 1 \end{bmatrix} $$
$$ \lambda_{2} = -2, v_{2} = \begin{bmatrix} 1 \\ -1 \\ 4 \end{bmatrix} $$
$$ \lambda_{3} = 3, v_{3} = \begin{bmatrix} -1 \\ 1 \\ 1 \end{bmatrix} $$
이렇게 얻어진 벡터들을 합치면 아래와 같이 $P$ 행렬을 구할 수 있습니다.
$$ P = \begin{bmatrix} -1 & 1 & -1 \\ 0 & -1 & 1 \\ 1 & 4 & 1 \end{bmatrix} $$
위의 $P$를 가지고 $P^{-1}$를 구해서 $P^{-1}AP$를 구하면 아래와 같은 값을 얻게 됩니다.
$$D = P^{-1} A P = \begin{bmatrix} 2 & 0 & 0 \\ 0 & -2 & 0 \\ 0 & 0 & 3 \end{bmatrix} $$
결과를 살펴보면, $P$를 구성할 때, eigenvector의 순서에 따라, eigenvalue가 위치하는 것을 볼 수 있습니다.
$$ P = \begin{bmatrix} v_{1} & v_{2} & v_{3} \end{bmatrix}, D = \begin{bmatrix} \lambda_{1} & 0 & 0 \\ 0 & \lambda_{2} & 0 \\ 0 & 0 & \lambda_{3} \end{bmatrix} $$
앞에서 배웠던 eigenvalue 구하는 방법을 통해서 대각화를 진행하는 방법까지 알아봤습니다. 다음 포스팅에서는 SVD와 orthogonal, orthonormal에 대해 소개해보려고 합니다. 조금이나마 도움이 되셨길 바랍니다.