[통계] 대응표본 비모수 검정방법 살펴보기(맥니마 검정, 코크란 Q검정)

들어가기 전에

 지난 포스팅에서는 비모수 검정과 모수 검정에 대한 간략한 소개를 했습니다. 그리고 사내에 새로운 교육을 실시하는 예시를 통해, 가설 검정하는 순서와 비모수 검정과 모수 검정을 했을 때의 차이에 대해서 다뤘습니다. 해당 내용이 궁금하시다면 여기를 클릭하시면 확인하실 수 있습니다.
 오늘은 지난 포스팅에서 소개하지 못한 맥니마 검정, 코크란 Q검정에 대해서 작성해보려고 합니다. 이 포스팅에서는 비모수 검정방법에 대한 간략한 소개, 각 가설검정 방법이 어떤 경우에 사용할 수 있는 지, 맥니마 검정과 코크란 Q검정에 대해서 알아봅니다. 대략적인 통계 배경지식이 있으신 분들이나 ADP 준비 중이신 분들에게 도움이 될 것 같습니다.

비모수 검정방법

 비모수 검정방법은 지난 포스팅에서 말했듯이, 모집단의 분포에 대해 가정하지 않고 검정하는 방법입니다. 주로 주어진 자료가 정규분포가 아니거나, 표본의 크기가 작거나 데이터가 서열척도나 명목척도인 경우에 사용합니다. 흔히 많이 알고 계신 검정방법에는 wilcoxon 순위 합 검정, Mann-whitney U 검정 등이 있습니다. 각각의 방법들이 어떤 경우에 사용되는지 모수검정방법과 같이 살펴보겠습니다.

 

가설 검정 방법 잘 사용하기

단일 표본 가설검정

 단일 표본 가설검정은 모집단의 평균/비율/중앙값에 대한 가설을 검정하는 방법입니다. 주로 모집단의 평균/비율/중앙값이 특정 값과 같은지를 검정하는 형태로 진행됩니다. 
 모수적인 방법에는 단일표본 t검정, 단일표본 z검정, 단일표본 비율 검정이 존재합니다. 각 방법들은 주어진 데이터 형태, 정보에 따라 다르게 사용됩니다. 평균값을 비교하는 경우 정규분포를 따르고 모집단의 표준편차를 안다면, Z검정을, 모집단의 표준편차를 모른다면 T검정을 사용하면 됩니다. 이진 변수로 모집단의 비율을 검정하기 위해서는 단일 표본 비율 검정을 사용할 수 있습니다.
 만약 정규분포를 따르지 않는다면, 부호검정을 활용하여 중앙값을 특정 값과 비교할 수 있습니다. 왜 비모수검정에서는 평균값을 사용하지 않고, 중앙값을 사용하는 것일까요? 보통 데이터가 정규분포를 따르지 않는 경우, 극단치를 포함하거나 비대칭적인 분포일 수 있습니다. 극단치를 포함하거나 비대칭적인 분포는 중앙값보다 평균값에 더 많은 영향을 주기 때문에 중앙값으로 비교하는 것이 합리적이라고 볼 수 있습니다. 

 

대응 표본 가설검정

 대응 표본 가설검정은 동일한 개체에서 추출된 두 표본의 평균/중앙값을 비교하는 방법입니다. 주로 동일한 집단에 대해 특정 실험을 하기 전/후를 비교하는 방법이 대표적입니다
 집단이 2개인 경우, 모수적인 방법에는 대응표본 T검정이 존재합니다. 대응표본 T검정은 정규분포를 따르고 등분산성을 만족한 경우에 사용할 수 있으며, 해당 조건들을 만족하지 못하는 경우에는 비모수 검정방법을 사용할 수 있습니다.
 비모수 검정방법에는 Wilcoxon 부호 순위 합 검정, 대응표본 맥니마 검정, 부호검정을 활용할 수 있습니다. Wilcoxon 검정방법의 경우 값이 연속형인 경우에 활용할 수 있고, 맥니마 검정은 이항적인 결과를 갖는 경우, 두 범주형 변수 간의 차이를 검정할 수 있습니다.
 집단이 3개 이상인 경우에는 기본적인 가설검정 이후에 사후 검정을 통해 어떤 집단간의 차이가 존재하는지 확인하는 과정이 추가됩니다. 모수적인 방법에는 Paired 분산분석(ANOVA)이 존재합니다. 세 개 이상의 처리 또는 조건 간의 평균 차이를 비교하는 방법입니다. 비모수적인 방법에는 Friedman 검정, 코크란 Q 검정방법이 존재합니다. Friedman 검정은 중앙값 검정을 할 때 사용하고,  코크란 Q검정은 두 가지 이상의 범주에 대한 차이를 비교할 때 사용할 수 있습니다.

 

독립 표본 가설검정

 독립 표본 가설검정은 이전 포스팅에서 소개한 것처럼 두개의 독립된 집단 간의 차이를 비교하는 방법입니다. 독립 표본 가설검정도 대응표본과 비슷하게 집단이 2개일 때, 3개 이상일 때 사용할 수 있는 검정방법이 다릅니다.
 집단이 2개인 경우, 모수적인 방법에는 독립표본 T검정과 Welch's t-검정을 활용할 수 있습니다. 독립표본  T검정을 사용하기 위해서는 정규분포이며, 등분산성이 만족된 경우에 사용할 수 있습니다. 만약, 등분산성이 만족되지 않는다면 Welch's t-검정을 사용하는 것이 더 적절합니다. 비모수적인 방법에는 Mann-whitney U 검정, 카이제곱 검정 방법 등을 활용할 수 있습니다. Mann-whitney U 검정은 두 집단 간의 중앙값 차이를 검정하고, 카이제곱 검정 방법은 범주형 자료의 독립성을 비교하는데 주로 활용합니다.
 집단이 3개 이상인 경우, 모수적인 방법에는 분산분석(ANOVA)이 존재합니다. 분산분석 비모수적인 방법에는 Kruskal-Wallis 검정 방법을 사용할 수 있으며, 집단 간의 중앙값의 차이를 비교할 때 사용합니다.

 대략적인 가설검정 방법들에 대해서는 소개했으니, 대응표본 가설방법의 맥니마 검정과 코크란 Q검정에 대해서 소개하겠습니다.

 

맥니마 검정

 위에서 언급했듯이, 맥니마 검정방법은 대응표본에서 범주형 자료에 대한 비모수 검정 방법입니다. 맥니마 검정을 하기 위해서는 교차표(cross-tab)가 필요합니다. 예를 들어, A라는 회사에서 새로운 알약을 개발했다고 해봅시다. 해당 회사에서 개발한 알약을 투여 전과 후로 증상이 호전되었는지 증상이 동일한지를 조사했다고 가정합시다. 약을 사용하기 전에 증상의 호전여부와 약을 사용한 후의 증상 호전여부를 파악하면 아래와 같은 결과와 교차표가 생성될 것입니다.

 

 위에서 얻어진 교차표를 활용해서 아래처럼 검정 통계량을 구할 수 있습니다.

 실제로 구해진 값을 가지고 파이썬으로 가설 검정을 진행하면 어떤 결과가 나오는 지 확인해 봅시다.

# 실제 계산 방법
import pandas as pd
from scipy.stats import chi2_contingency, chi2

# 약 투입 전 후 데이터
table = pd.DataFrame([[3, 1], [4, 2]], index=['약 투입 전 호전', '약 투입 전 증상 동일'], columns=['약 투입 후 호전', '약 투입 후 증상 동일'])
print(table)

b = table.values[0][1]
c = table.values[1][0]
stat = (b-c)**2/(b+c)
df = 1
pval = 1 - chi2.cdf(stat, df)
print(pval)

# 유의수준 0.05에서의 검정결과
alpha = 0.05
if pval < alpha:
    print("귀무가설을 기각합니다. 약 투입 후 효과가 있습니다.")
else:
    print("귀무가설을 기각하지 않습니다. 약 투입 후 효과가 없습니다.")
    
    
# 라이브러리 활용
from statsmodels.stats.contingency_tables import mcnemar
mc = mcnemar(table.values, exact=False, correction=False)
# exact=True : binomial distribution, exact=False : chisquare distribution
# correction : 카이제곱(연속 분포), 맥니마 검정은 이진 분포를 근사치로 사용하므로 일부 오차 발생 가능. 연속성 보정 옵션
print(mc.statistic, mc.pvalue)

 위 예시로 사용한 경우에는 p-value가 0.1797로 0.05보다 크므로 귀무가설을 기각하지 않습니다. 이처럼, 프로모션을 도입 후에 전/후 차이 등을 확인할 때 유용하게 사용할 수 있는 검정 방법입니다.

 

코크란 Q검정

 코크란 Q검정은 대응표본 이항변수로 되어 있는 3개 이상의 변수 간 비율 차이를 검정하는 방법입니다. 예를 들어, A회사에서 상품을 판매하기 위해 판매전략 3개를 사용하고 있다고 했을 때, 판매 전략에 따라 판매 효과가 있는지 검정해야 하는가를 검정한다고 해봅시다.

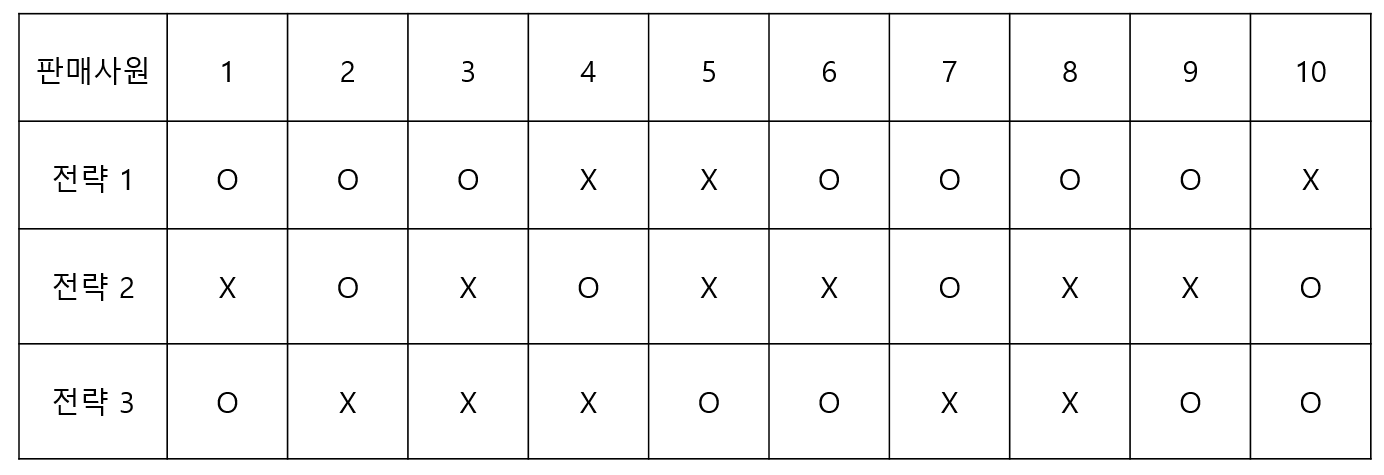
각 판매사원 10명에게 전략 3개로 판매성공한 결과와 실패한 결과를 수집했다고 해보자. 각 판매전략 종류에 따라 어떤 차이가 있는 지 살펴보기 위해서 코크란 Q검정을 진행해 봅시다.

 코크란 Q 검정의 통계량을 구하기 위해서는 표본의 개수(k, 전략), 샘플 수(n, 판매사원 수), 각 전략별 합계, 각 사원별 합계를 통해 구할 수 있습니다. 아래는 파이썬 코드로 실제 구한 값입니다.

#H0 : 모든 판매전략에 대한 판매비율은 차이가 없다.
#H1 : 적어도 한 개의 판매전략 판매비율은 차이가 있다.
import numpy as np
from scipy.stats import chi2

# 샘플 데이터
strategy1 = [1, 1, 1, 0, 0, 1, 1, 1, 1, 0]
strategy2 = [0, 1, 0, 1, 0, 0, 1, 0, 0, 1]
strategy3 = [1, 0, 0, 0, 1, 1, 0, 0, 1, 1]
table = pd.DataFrame([strategy1, strategy2, strategy3], index=['판매전략1', '판매전략2', '판매전략3'], columns=[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]).transpose()

# 코크란 검정 방법 (소스코드 참고)
n = table.shape[0]
k = table.shape[1]
df = k-1
k_sums = np.array(table.sum())
print(k_sums)
n_sums = np.array(table.sum(axis=1))
print(n_sums)
q1 = (k * sum(k_sums**2)) - sum(k_sums)**2
q2 = k * sum(n_sums) - sum(n_sums**2)
stat = (df * q1) / q2
pval = 1 - chi2.cdf(stat, df)
print(stat, pval)
alpha = 0.05
if pval < alpha:
    print("귀무가설을 기각합니다. 적어도 1개의 판매전략에 대한 판매비율은 차이가 있다.")
else:
    print("귀무가설을 기각하지 않습니다. 모든 판매전략에 대한 판매비율은 차이가 없다.")
    
# 라이브러리 활용
cq = cochrans_q(table)

# 결과 출력
print("코크란 Q 통계량:", cq.statistic)
print("p-value:", cq.pvalue)

# 유의수준 0.05에서의 검정결과
alpha = 0.05
if cq.pvalue < alpha:
    print("귀무가설을 기각합니다. 적어도 1개의 판매전략에 대한 판매비율은 차이가 있다.")
else:
    print("귀무가설을 기각하지 않습니다. 모든 판매전략에 대한 판매비율은 차이가 없다.")

 위 데이터를 기반으로 가설검정한 결과 p-value가 0.4965로 귀무가설을 기각하지 않습니다. 결론, 모든 판매전략에 대한 판매비율에는 차이가 없다고 볼 수 있습니다. 만약, 여기서 p-value가 0.05보다 낮아서 기각하게 된다면, 모든 쌍에 대해서 맥니마 검정을 진행(사후검정)하여 차이가 있음을 확인하면 됩니다. 이 방법은 현업에서 공장별 불량률을 비교 분석하기 위해서 사용될 수 있는 방법으로 유용할 것으로 보입니다.

 

3줄 정리하기

• 맥니마 검정은 대응표본에서 범주형 변수인 경우에 활용할 수 있는 비모수 검정방법입니다.
• 코크란 Q검정은 대응표본에서 이항 변수로 3개 이상의 표본이 존재할 때 활용할 수 있는 비모수 검정방법입니다.
• 단순히 제품의 합/불 정보가 있는 제조업, 프로모션 도입 등의 마케팅 분야에서도 활용해 볼 수 있을 것 같습니다.