본문 내용은 cs231n의 유튜브를 기반으로 작성되었음을 알려드립니다.
해당 유튜브 강의를 들으시고 싶으시다면 여기를 클릭하세요.
자료 출처: http://cs231n.stanford.edu/slides/2017/cs231n_2017_lecture10.pdf
1. Recurrent Neural Networks
순환 신경망(RNN, Recurrent Neural Networks)은 순서가 있는 데이터(sequence data)를 학습하기 위한 인공신경망입니다. 오늘 Lecture10에서는 RNN의 원리에 대해서 배우게 됩니다.

RNN을 적용하는 문제에 대해 설명하면서 위의 그림같이 5가지로 분류하여 설명했습니다. 빨간색은 input layer, 초록색은 hidden layer, 파란색은 output layer입니다. 위의 내용을 아래에서 설명해보겠습니다.
첫 번째, one to one은 입력과 출력이 1개인 것으로 대표적으로 Vanilla Neural Network가 있습니다. Vanilla Neural Network는 가장 기본적인 네트워크를 말합니다. 여기서 Vanilla는 바닐라향을 쓴 아이스크림으로 가장 흔하고 아이스크림의 기본이라 할 수 있을 정도로 '표준'이라는 느낌을 줍니다. 그래서 Vanilla라는 단어를 사용한 것 같습니다.
두 번째, one to many는 입력은 1개, 출력은 여러 개인 방법으로 대표적인 예로 이미지 캡셔닝(image captioning)이 있습니다. 이미지 캡셔닝은 이미지를 단어로 설명하는 기술을 말합니다. 이때, input으로는 이미지가 들어가며, 이미지 내부의 물체들에 대해 여러 개의 단어로 변환하여 설명하게 되기에 one to many의 한 예라고 볼 수 있습니다.
세 번째, many to one은 입력은 여러 개, 출력은 하나인 방법입니다. 예를 들면, "나는 오늘 육개장을 먹어서 행복하다."라는 문장을 input을 받아서 output으로 "행복"과 같은 감정을 출력하는 감정 분류(setiment Classification)이 대표적인 방법입니다.
네 번째, many to many는 두 가지로 나눠지는 데, 전자의 대표적인 것은 번역(Machine Translation)이 있습니다. 나라마다 언어의 길이나 크기가 다르기 때문에 입력의 크기와 출력의 크기가 다를 수 있습니다. 후자의 경우 비디오 분류(Video classification)를 예로 들 수 있습니다.
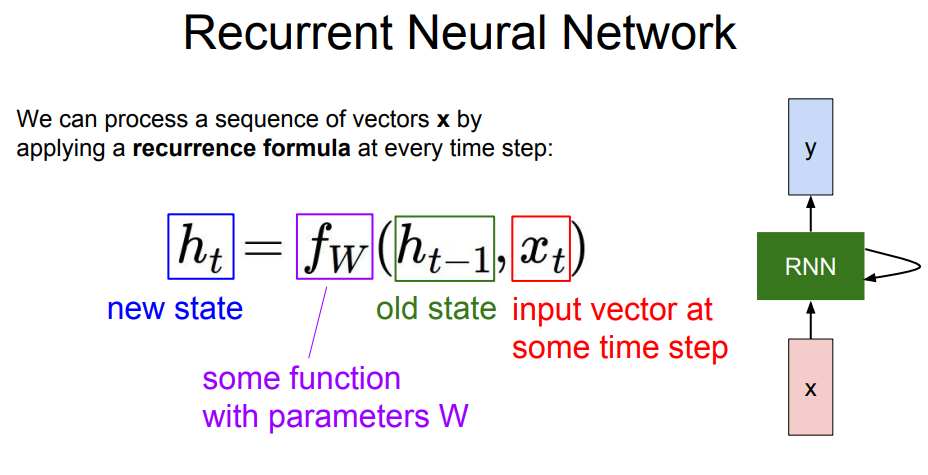
위의 그림에서는 RNN의 기본적인 원리에 대해서 설명하고 있습니다. 보시는 것처럼 RNN은 모든 time step에서 재귀식/점화식(recurrence formula)을 적용해서 작동하게 됩니다. 점화식(recurrence formula)은 이웃하는 두개의 항 사이에 성립하는 관계를 나타낸 식을 말합니다.
위의 식에 적용해보면 $h_t$에 대한 점화식이라고 볼 수 있습니다. RNN은 t시점의 새로운 상태인 $h_{t}$를 old state인 $h_{t-1}$와 t시점의 input vector인 $x_t$에 의해 구할 수 있습니다. 여기서 특징적인 것은 모든 RNN에서는 동일한 function과 파라미터 W를 사용해야 한다는 것입니다.

Vanilla RNN에서는 위에서 보시는 것처럼 tanh함수를 사용했습니다. tanh함수는 비선형성을 위해 적용하게 되었는데, 선형함수를 사용하게 되면, 층을 거치면서 크게 변화가 발생하지 않습니다. tanh함수는 RNN의 gradient가 최대한 오래 유지할 수 있도록 해주는 역할로 사용됩니다. 자세한 설명은 여기를 클릭하세요.
여기서 사용된 $W_{hh}$는 h와 h 사이의 파라미터, $W_{xh}$는 x에서 h 사이의 파라미터, $W_{hy}$는 h에서 y 사이의 파라미터로 사용됩니다. 여기에 있는 파라미터들은 위에서도 언급했듯이 모든 타임 스텝에서 동일한 값을 가집니다.
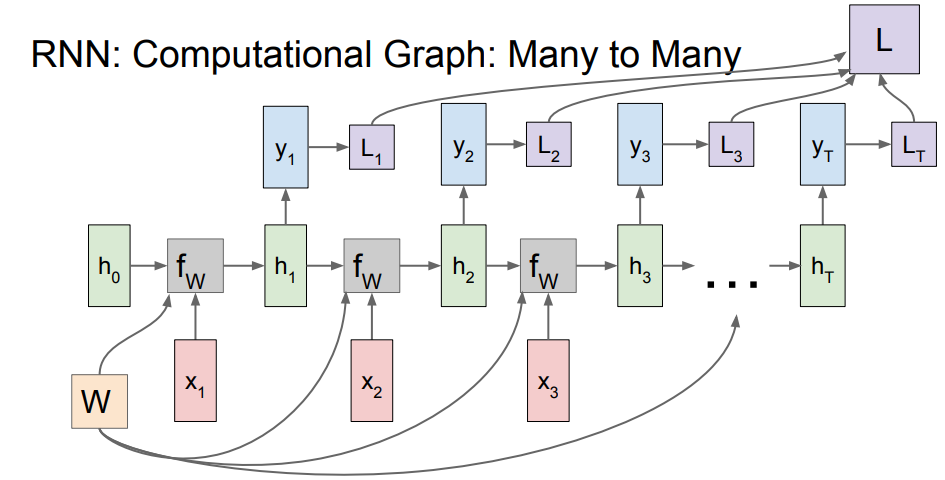
위의 그림은 Many to many의 경우에 해당되는 계산 그래프(Computational Graph)입니다. 위의 흐름처럼 계산이 되고, 각 타임 스탭에서 생성된 loss들의 합이 RNN 전체의 loss값이 됩니다.
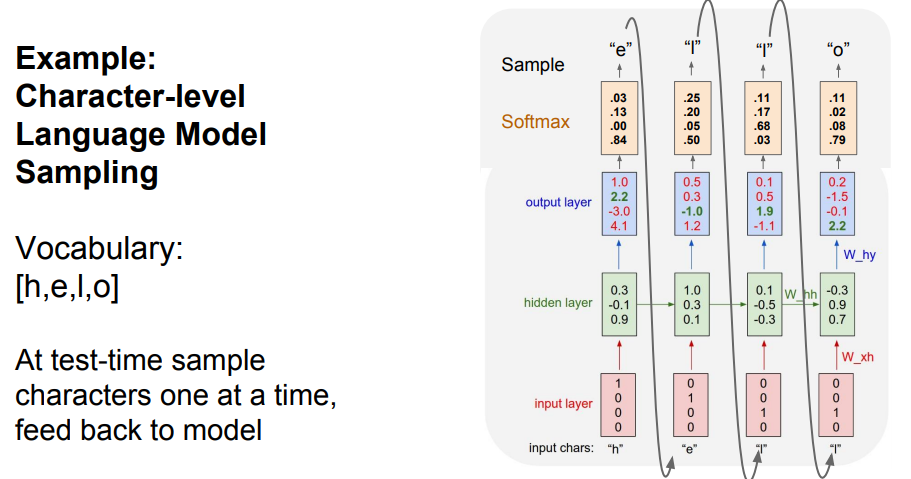
위의 그림은 "hello"라는 sequence data를 주고, 정답을 찾을 수 있는 지 확인하는 예시입니다. 여기서 저희가 사용할 알파벳은 4개이므로, 4개를 각각 원-핫 인코딩을 통해 벡터화해서 Vocabulary에 저장했습니다. 그리고 input으로는 "h"를 넣었을 때에는 "e"가 출력되고, "e"를 입력으로 넣었을 때에는 "l"이 출력되도록 만듭니다. 위의 예시는 Vanilla RNN이므로 tanh함수를 활용했습니다. 최종 결과 쪽을 보시면, 이상한 것을 알 수 있습니다. "e"는 [0,1,0,0]이지만, output layer에서는 [1, 2.2, -3, 4.1]로 4.1이 가장 큰 값인 것을 확인할 수 있습니다. 하지만, 가장 큰 값을 출력하는 것이 아닌 샘플링을 통해서 값을 출력하게 됩니다. 때로는 argmax가 좋을 때가 있지만, 샘플링을 통해 모델에서 다양성을 얻을 수 있다는 장점이 있습니다. 예를 들면, "e"가 나오면 무조건 "l"이 아닐 수도 있습니다. 이처럼, 다양성을 위해 샘플링으로 최종 값을 출력합니다.
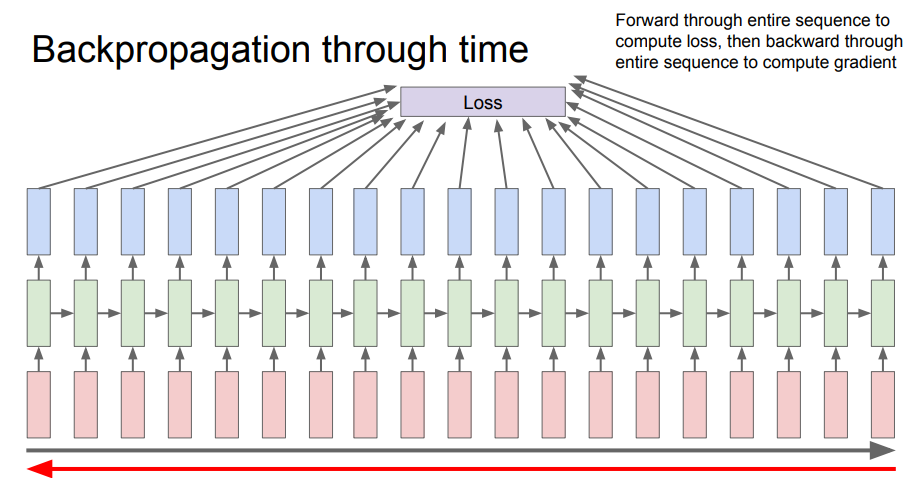
RNN에서의 단점은 backpropagation을 구하기 위해서는 Forward로 전체의 sequence를 계산한 뒤에 backward를 적용해야 한다는 것이다. 이것은 시간의 순서대로 진행되기 때문에 시간이 오래걸린다. 이를 극복하기 위해서 아래의 그림처럼 미니 배치로 적용하는 방법이 있습니다.

이런 RNN을 활용해서 다양한 예시를 보여줬습니다. 셰익스피어의 글을 넣어서 학습되는 과정을 표현했는데, 자세히 보지 않으면 영어라고 믿을 정도의 학습능력을 볼 수 있었습니다. 이 외에도 수학증명, C언어 코딩 등을 학습시킨 흥미로운 결과를 확인할 수 있었습니다.
2. 이미지 캡셔닝(Image Captioning)

이미지 캡셔닝은 사진을 입력으로 받아 사진을 단어로 설명하도록 하는 기술을 말합니다. 여기서는 저희가 앞서 배웠던 CNN과 RNN을 함께 활용합니다.
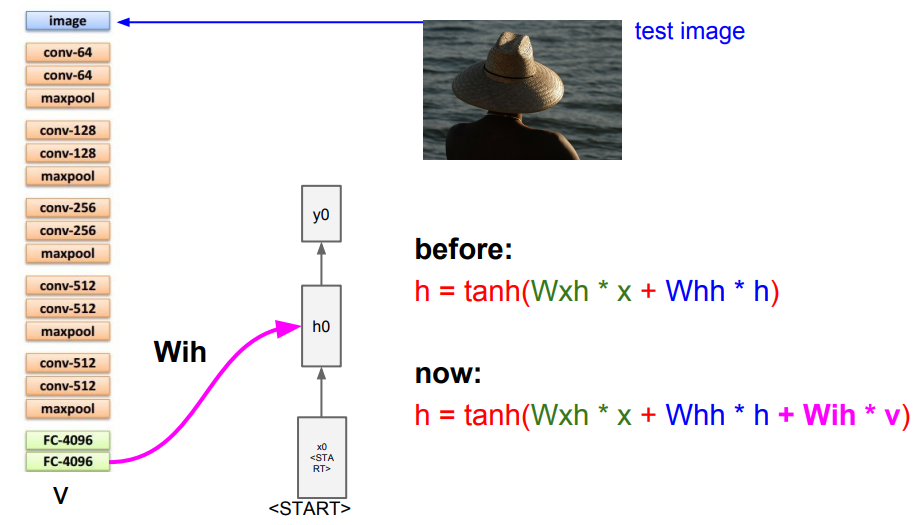
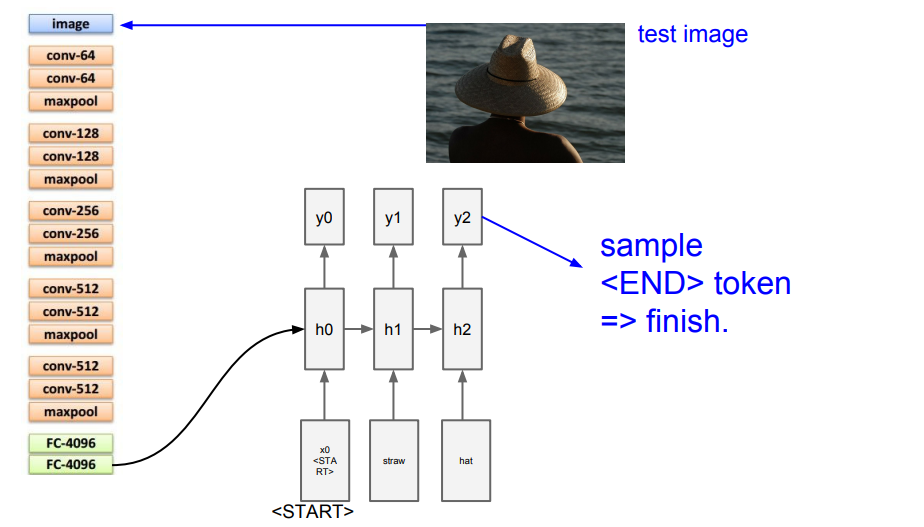
이미지 캡셔닝의 과정은 위에 보시는 그림과 같이 진행이 됩니다.
이미지 캡셔닝 과정
(1) 이미지를 입력으로 받습니다.
(2) CNN을 지나면서 해당 이미지에 대한 요약된 벡터 값을 받습니다. 이때, 기존 CNN의 마지막에 있는 softmax는 제거된 상태입니다.
(3) 받은 값을 기존 Vanilla RNN식에 추가하여 계산하게 됩니다. 처음 x0값은 START라는 토큰 값이 주어지게 되고, 모든 단어를 RNN을 통해 출력합니다.
(4) 마지막에 더 이상 출력할 것이 없으면 END 토큰으로 종료되게 됩니다. 이미지 캡셔닝에서는 마지막에 END 토큰을 출력하는 것도 학습을 시켜줘야 합니다.
이를 이용한 결과, 생각보다 좋은 문장을 만들지만 때로는 이상하게 묘사가 되기도 합니다.

이 방법은 위의 이미지 캡셔닝에서 더 발전된 방법입니다. 수행방법은 위에 보시는 그림과 같습니다.

기존의 이미지 캡셔닝과 다른 점은 캡션 하는 위치까지 계산하는 점이 다르다고 볼 수 있습니다.

위의 사진은 soft attention과 hard attention 비교한 사진입니다. 하얀색으로 칠한 부분이 캡션 한 위치가 되겠습니다. soft attention은 hard attention에 비해 좀 더 넓은 범위에 대해 캡션을 하는 것을 알 수 있습니다.

위의 사진은 attention방법을 활용해서 질문과 사진 input으로 이에 해당하는 답을 찾는 방법입니다.
3. LSTM

LSTM을 설명하기 전에, 지금까지는 hidden layer가 1층인 것들에 대해 설명했습니다. 하지만, 여기서는 여러개의 층으로 이뤄진 Multilayer RNN의 모습을 볼 수 있습니다. 층이 깊어질수록 모델의 성능이 좋아지기 때문입니다. 최근에는 RNN보다 LSTM이 많이 사용되는데, 그 이유는 기존의 RNN이 갖는 장기 의존성 문제가 있기 때문입니다. 장기 의존성 문제는 은닉층의 과거의 정보가 마지막까지 전달되지 못하는 현상을 의미합니다. 이 현상은 경사도가 사라지는 현상이므로 vanishing gradient 문제라고도 합니다.
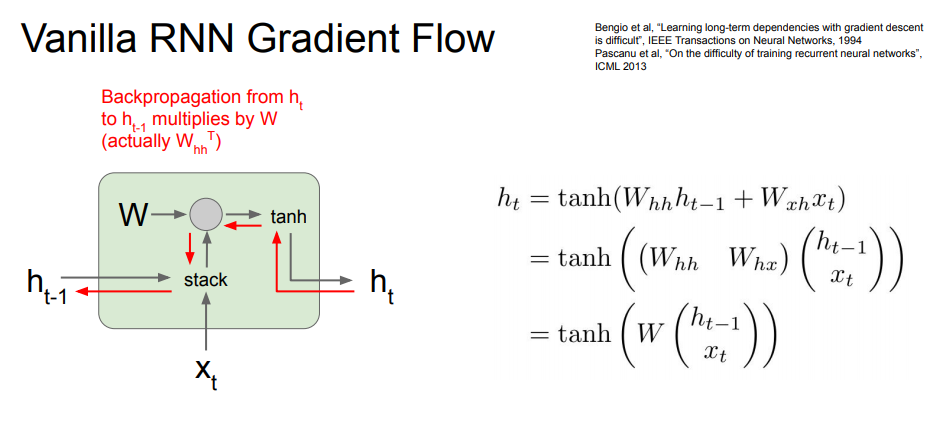
RNN에서도 CNN과 동일하게 성능 개선을 위해 backpropagation으로 weight를 업데이트 하게 됩니다. 이때, 위와 같은 흐름으로 진행이 됩니다.
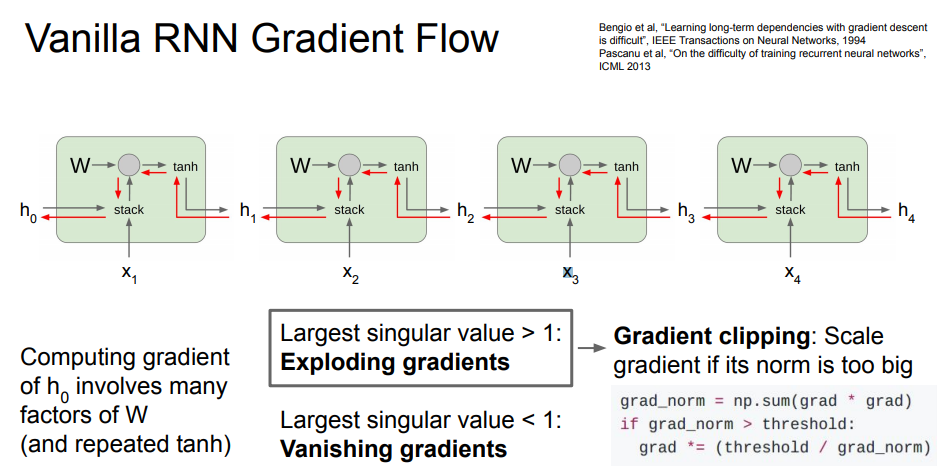
위의 그림처럼 똑같은 RNN이 계속 이어져있는 상황에서 2가지 문제가 발생하게 됩니다. 가장 먼저 RNN을 통해 backward pass 과정에서 weight의 일부 값과 곱해지는 상황이 생기게 되는 데, 이 중 동일한 RNN을 거치면서 수많은 가중치 행렬과 곱셈이 이뤄지게 됩니다. 여기서 가중치 행렬의 값 중 가장 큰 것이 1보다 크다면, loss값이 exploding 하는 현상을 만들게 됩니다. 이 문제는 우측에 보이는 것처럼 Gradient clipping으로 막을 수 있습니다. 하지만, 가장 큰 값이 1보다 작게 된다면, 가중치 행렬에 의해 점점 작아져서 0이 됩니다. 이와 같은 vanishing gradient 문제는 다른 구조의 RNN을 사용하는 것 밖에는 막을 수 있는 방법이 없습니다. 그래서 이를 보완하고자 나온 것이 LSTM이라는 방법입니다.

LSTM에서는 hidden state에 cell state를 추가한 구조로, i,f,o,g라는 게이트가 활용됩니다. 이 게이트는 각각 아래와 같은 특징을 가지고 있습니다.
게이트에 대한 설명
i(input gate) : 현재 정보를 얼마나 사용하는 지에 대한 게이트
f(forget gate) : 이전의 정보를 얼마나 잊어버릴 것인지에 대한 게이트
o(output gate) : 얼마나 드러낼 것인가에 대한 게이트
g(gate gate) : input을 얼마나 포함시킬 것인지에 대한 게이트
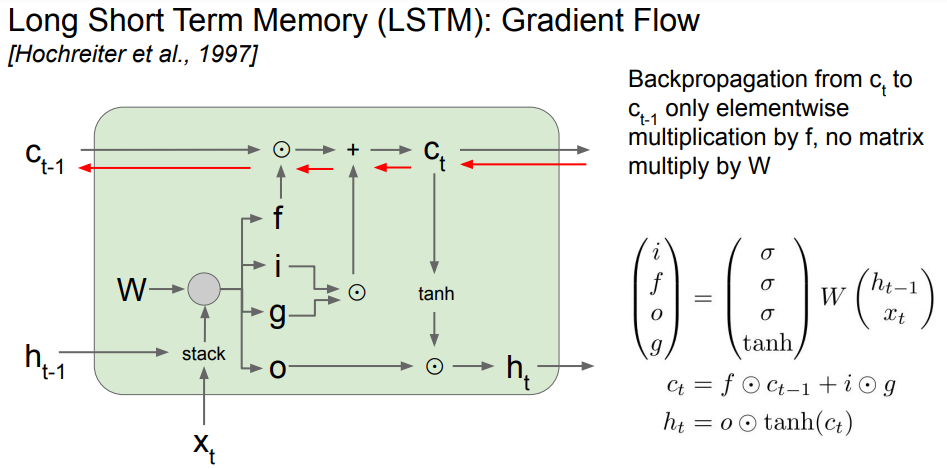
LSTM의 흐름은 아래와 같습니다.
LSTM forward pass 흐름
(1) $h_{t-1}$과 $x_{t}$의 값을 $W$와 곱한 다음, 시그모이드로 나온 값을 $f_{t}$인 forget gate(0~1 사이 값)를 $c_{t-1}$에 곱해줍니다.
(2) $i_{t}$는 $f_{t}$와 비슷한 과정으로 계산하고 $g_{t}$는 $h_{t-1}$과 $x_{t}$의 값을 $W$와 곱한 다음, $tanh$로 계산한 값을 hadamard product 곱을 한 것을 $c_{t-1}$와 forget gate 곱한 값에 더해줍니다.
(3) (2)에서 구한 값이 $c_{t}$로 업데이트가 됩니다.
(4) $c_{t}$를 $tanh$를 통해 -1~1의 값으로 바꾼 뒤 output gate와 곱해서 $h_{t}$값을 업데이트 해줍니다.

위의 그림처럼 cell state를 활용하면 정보를 최대한 잃지 않은 상태로 gradient값을 구할 수 있습니다. 이러한 모습은 마치 ResNet과 같다고 합니다.

LSTM과 같이 현재 유용하게 사용되고 있는 GRU라는 방법도 존재합니다.

Reference